Is Perfect Precision Possible?
I have mentioned in a previous article that perfect precision
(concurrency at the triple intersections) was not possible when
drawing the Sri Yantra by hand or even when using a computer.
The reasoning behind this statement comes from the method that has
been used to solve the geometry mathematically. The incremental
approach that has been devised so far is achieved by iterated
approximation as shown in the paper from C.S. Rao. This approach
allows one to get very close to perfection but never quite reaches it in
a mathematical sense. The errors can be made infinitely small, but
they still exist.
There are a multitude of methods to draw the figure by hand, but none
has ever achieved perfect precision either. Here again we are talking
about mathematical precision, not visual precision. It is certainly
possible to make a hand-drawn figure where the errors are smaller
than the thickness of the lines used in the drawing. This has the effect
of hiding the concurrency errors. However if the drawing was scaled
up, the errors would eventually show up as can be seen in the
animation below.
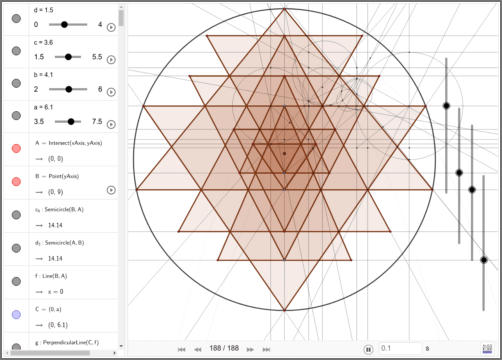
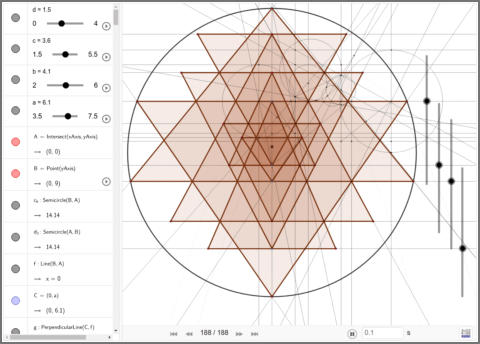
The best tool to test the precision of hand-drawn methods is
Geogebra, a simple and free drawing software that allows to draw
geometries in a very exact way. Geogebra is different from most other
drawing softwares in that it uses equations to represent points, lines,
circles, etc. This makes it possible to draw geometric figures with
perfect mathematical precision.
Alessandro Chiodo, a mathematician from the Institute of Mathematics
of Jussieu in Paris, appears to have succeeded in finding a method to
hand-draw the Sri Yantra without any errors by using the Apollonius
solution to the circle-line-point problem.
Problem of Apollonius explained here and an interactive
demonstration here.
This is a major achievement. This has never been done before as
far as I know. The paper by Chiodo details the method used to
produce a perfectly concurrent Sri Yantra by hand (rule and compass
method). Note that the first section of the paper is in French
(summary) but the rest is in English.
I have to warn the reader that the method is fairly complex and
requires a great deal of patience and attention to details to be
completed successfully. An easier way is to use the interactive
Geogebra drawing at the end of this article.
Using this method I was able to generate a vector Sri Yantra with
perfect concurrency.
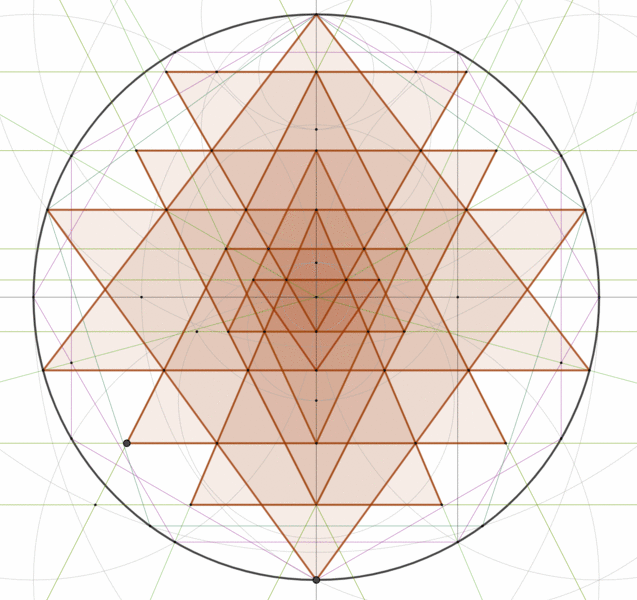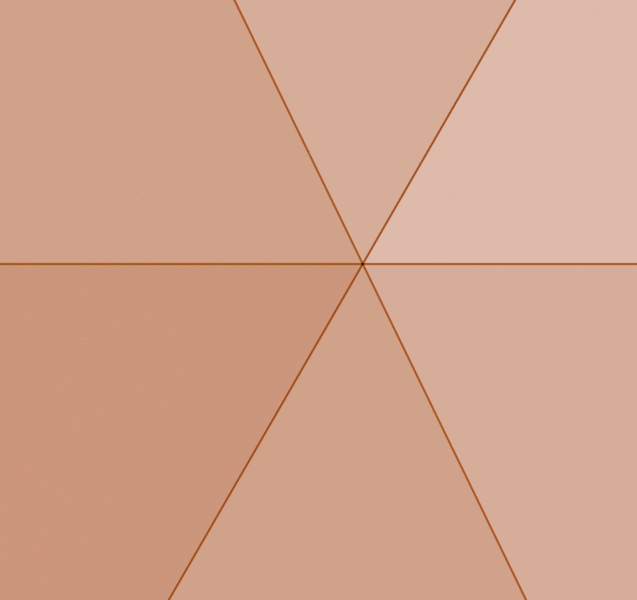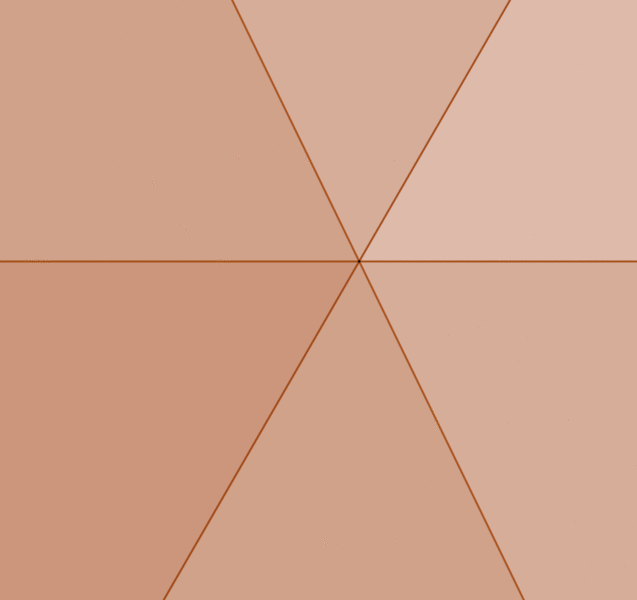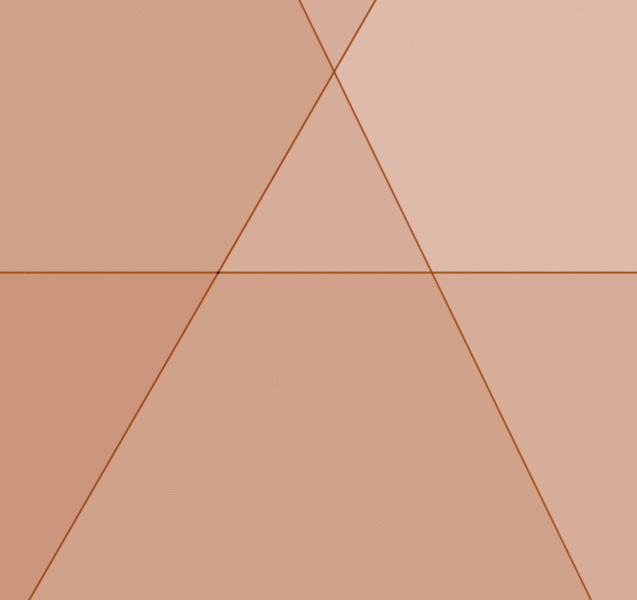
The animation below from Chiodo shows the entire drawing method:
Click on the image below to see his interactive Geogebra drawing of
the Sri Yantra.
Is Perfect Precision Possible?
I have mentioned in a previous article that perfect precision
(concurrency at the triple intersections) was not possible when
drawing the Sri Yantra by hand or even when using a computer.
The reasoning behind this statement comes from the method that
has been used to solve the geometry mathematically. The
incremental approach that has been devised so far is achieved by
iterated approximation as shown in the paper from C.S. Rao. This
approach allows one to get very close to perfection but never quite
reaches it in a mathematical sense. The errors can be made
infinitely small, but they still exist.
There are a multitude of methods to draw the figure by hand, but
none has ever achieved perfect precision either. Here again we are
talking about mathematical precision, not visual precision. It is
certainly possible to make a hand-drawn figure where the errors are
smaller than the thickness of the lines used in the drawing. This has
the effect of hiding the concurrency errors. However if the drawing
was scaled up, the errors would eventually show up as can be seen
in the animation below.
The best tool to test the precision of hand-drawn methods is
Geogebra, a simple and free drawing software that allows to draw
geometries in a very exact way. Geogebra is different from most
other drawing softwares in that it uses equations to represent
points, lines, circles, etc. This makes it possible to draw geometric
figures with perfect mathematical precision.
Alessandro Chiodo, a mathematician from the Institute of
Mathematics of Jussieu in Paris, appears to have succeeded in
finding a method to hand-draw the Sri Yantra without any errors
by using the Apollonius solution to the circle-line-point problem.
Problem of Apollonius explained here and an interactive
demonstration here.
This is a major achievement. This has never been done before as
far as I know. The paper by Chiodo details the method used to
produce a perfectly concurrent Sri Yantra by hand (rule and
compass method). Note that the first section of the paper is in
French (summary) but the rest is in English.
I have to warn the reader that the method is fairly complex and
requires a great deal of patience and attention to details to be
completed successfully. An easier way is to use the interactive
Geogebra drawing at the end of this article.
Using this method I was able to generate a vector Sri Yantra with
perfect concurrency.
The animation below from Chiodo shows the entire drawing
method:
Click on the image below to see his interactive Geogebra drawing
of the Sri Yantra.