Solving the Sri Yantra

The Quest for the Optimal Configuration
Nine Triangles in a Circle
Interconnections
The First Key: Concurrency
The One and the Many
The Second Key: Concentricity
The Third Key: Equilateral Inner Triangle
Center of Mass
The Sri Yantra from Sringeri Temple
The Three Flavors of the Sri Yantra
The Optimal Sri Yantra
The Quest for the Optimal Configuration
If you have ever attempted to draw this figure you already know that it is a lot more difficult to draw than you might have thought at first. The reason for this is mainly because the triangles are interconnected. If you move one, you need to move all the others so that they will intersect properly. With enough time or with the aid of computers and mathematics it is possible to draw a figure where the intersections match perfectly.
But it turns out that this is not enough to fully define the figure. This criteria in itself is not enough to produce a unique figure. This is the reason why there are so many different versions of the Sri Yantra in circulation.
Surprisingly the methods that we have found in the Indian literature are far from satisfactory. They often lead to very imprecise and crude figures. They only provide a rough idea of what the figure should look like. Contemporary methods can lead to more precise figures but they are all slightly or greatly different.
This begs the question: what is the proper configuration of the Sri Yantra? The goal of this article is to investigate the geometry of the Sri Yantra and see if we can find out more about this fascinating sacred figure. Join us on the quest for the optimal Sri Yantra.
Questions that will be answered in this article:
- What is the Sri Yantra?
- Why is it so difficult to draw?
- Why are there so many different versions?
- What are the characteristics that define an optimal figure?
- What is a Meru (pyramidal) Sri Yantra?
- What is a Kurma (spherical) Sri Yantra?
- How can I get an optimal Sri Yantra figure?
 |
 |
 |
 |
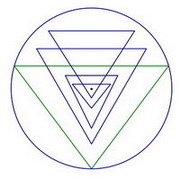
Four triangles pointing up.
|
Five triangles pointing down |
Central figure |
Complete Sri Yantra |
Figure 1 |
|||
The Sri Yantra is composed of a central figure that is surrounded by two circular rows of petals and then by a rectangular enclosure called the bhupura. In this study we will be focusing mainly on the central figure which is composed of nine overlapping triangles and a bindu point. Four of the triangles point up, the other five point down. In the most popular configuration the two biggest triangles (green triangles in figure 1) touch the outer circle on all three points. In some other versions there are either one or two more triangles that touch the outer circle (See figure 5).
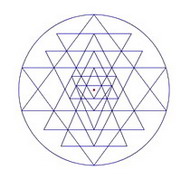
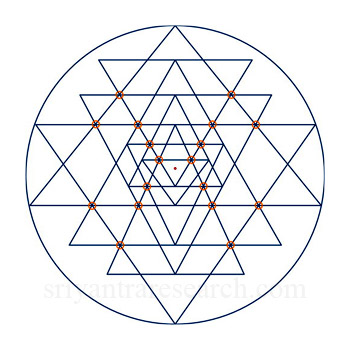 |
| Figure 2 Triple intersections. |
When looking at the figure we notice that there is a high degree of interconnectedness between the nine triangles. This the main reason why it is so difficult to draw. This means that every triangle is connected to one or more of the other triangles via common points. Changing the location of one of the triangle usually requires changing the size and position of many other triangles.
Figure 2 shows where the triple intersection points are located. These are the points that lock together the triangles. You can't move one without also moving the others.
Notice also that the two biggest triangles are touching the outside circle on three points and that the apex of every triangle is connected to the base of another triangle.
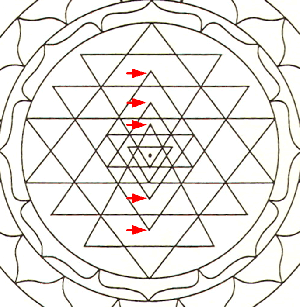 |
Figure 3 False Sri Yantra |
As with everything else there is a tendency to simplify and/or distort things , so that over time knowledge gets eroded. In the case of the Sri Yantra this has led to what some call the "false Sri Yantra". It's a version that is so far from the original figure that it is missing some of the most basic characteristic of a Sri Yantra. An example of such a false Sri Yantra is shown in figure 3. Here we see that the apex of most triangle is not connected with the base of another triangle as indicated by the red arrows. This reduces greatly the difficulty of drawing the figure and leads to something that looks like a Sri Yantra but isn't.
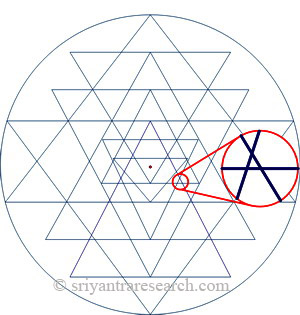 |
| Figure 4 Errors in the drawing will lead to extraneous secondary triangles. |
The obvious challenge when drawing a Sri Yantra is to achieve near perfect concurrency. Meaning that all the triple intersection meet at the same point rather than crisscrossing.
Figure 4 shows a detail of a Sri Yantra with the error circled in red. The lines should intersect at the same point but instead they crisscross each other and form an extraneous triangle. Using the right sequence to draw the Sri Yantra will ensure that there will be errors only in two of the triple intersections.
Very few Sri Yantras achieve perfect concurrency. Mathematically speaking it is not possible. But practically speaking a satisfactory level of precision can be achieved. It is difficult to achieve this when doing the drawing by hand but not impossible. Often the lines are made thicker to hide the errors at the intersections. A good level of accuracy can be achieved with a pencil and ruler and a lot of patience. A better accuracy can be achieved with a drawing program such as AutoCAD or Visio. The greatest amount of accuracy will be achieved by using a mathematical program such as Mathematica to compute the figure.
 |
 |
 |
| Figure 5 Three different configurations of the Sri Yantra. |
||
It would seem at this point that all one needs to do is to make sure that the lines match precisely at the triple intersections (concurrency) and our job is done. Not so!
Why are there so many different versions of the Sri Yantra out there? Figure 5 shows a few examples of Sri Yantras. In these examples the differences are obvious. The differences are usually more subtle and require closer examination. Like snow flakes there seems to be an infinite number of different Sri Yantras. Why is that? How can that be? Isn't there a precise and complete method that would tell us how this famous sacred figure should be drawn? If there is one we haven't found it yet.
The reason is simple. The criteria of concurrency (precise intersections) is not enough to fully define the Sri Yantra. Over time people have assumed that being able to produce a figure where the lines meet precisely at the intersections will produce a unique figure. This has lead to the current multiplicity of figures available.
Let us take the simple example of drawing a triangle. If the only criteria required is that the figure must have three sides then you can draw a infinite number of different triangles with three sides. If on the other hand you are asked to draw a triangle where the sides are of equal length then there is only one way to draw such a triangle (not taking size into account).
The Sri Yantra is a geometry with five degrees of freedom, which means that up to five different criterion can be used to define it. This is why we have to decide on the location of five lines when drawing the figure. Five degrees of freedom is not a lot considering that there is a total of nine triangles. This is because of the high degree of interconnectedness between the triangles. This effectively limits the possibilities and variations that can be achieved.
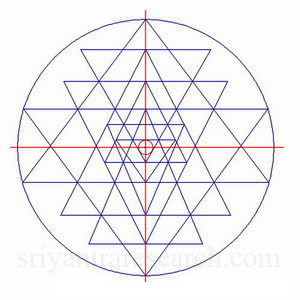 |
| Figure 6 Concentricity: the center of the innermost triangle coincide with the center of the outer circle. |
Lets now take a look at the bindu point; the small point located in the central triangle. It should be located in the center of the innermost triangle. This can be achieved precisely by placing the bindu at the center of a circle that fits inside this triangle (see figure 9). This is known in mathematics as the incenter of a triangle.
To achieve a perfectly centered figure however, the bindu should also be located at the center of the outer circle. This is illustrated in figure 6. The red cross shows where the center of the outer circle is located. The small red circle shows where the center of the innermost triangle is. As we can see in this figure they coincide. This is not the case for most Sri Yantras.
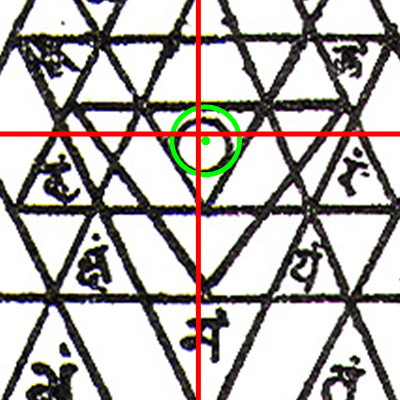 |
| Figure 7 Sri Yantra that doesn't meet the concentricity criteria. |
Figure 7 shows an example of a Sri Yantra where the center of the innermost triangle doesn't match perfectly with the center of the outer circle. The green dot (center of the innermost triangle) is not aligned with the center of the red cross (center of the outer circle).
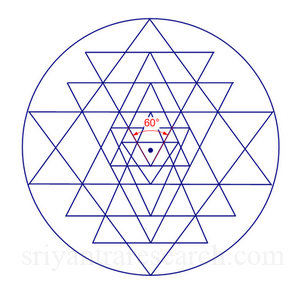
The Third Key: Equilateral Inner Triangle
 |
| Figure 8 R. Buckminster Fuller stands in front of his geodesic dome. |
The equilateral triangle is a perfect and minimal structure. It is the simplest, strongest and most fundamental structure in geometry and computer graphics. It has the highest degree of tensegrity for a minimum amount of structural elements. That is why it is so prevalent in the structural designs created by Buckminster Fuller. This is also why the geodesic dome, a spherical structure composed of small triangles is the only man-made structure that becomes proportionally stronger as it increases in size.
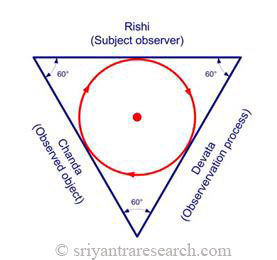 |
| Figure 9 Equilateral triangle as the expression of Rishi, Devata, Chanda. |
The Sri Yantra symbolizes, among other things the unfoldment of creation. The bindu represents the unmanifest, the silent state. The next level in the expression of the Universe is represented by the innermost triangle. This level represents the trinity of rishi, devata, chanda, or the observer, the process of observation and the object being observed. At this point the symmetry of creation is still intact and will be broken when it reaches the next level which represent the grosser aspects of the relative.
This reflects the unfoldment from unity to trinity as expounded in the Vedic literature. According to the Veda the Universe becomes manifest when unbounded awareness becomes aware of itself. The spark of self awareness ignites creation. At this point Unity divides into the trinity of rishi (the observer), devata (process of knowing) and chanda (the object of perception). The same idea is also found in the bible as the principle of the holy trinity.
The central triangle is the central lens of the Sri Yantra. If as some suggest, this pattern is capable of emitting a significant amount of subtle energy, the importance of having a well balanced and centered figure becomes obvious.
For these reasons we believe that the central triangle should be equilateral in an optimal Sri Yantra configuration. For this to happen the highest down pointing primary triangle must have an angle of 60 degrees (see figure 9 and 11).
 |
 |
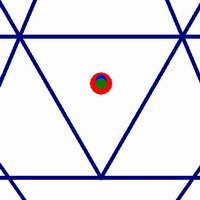 |
Figure 10 |
||
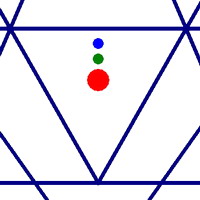
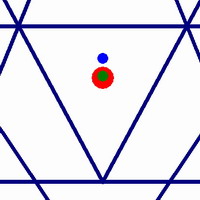
Now lets see if we can find ways to confirm the idea that we are getting closer to a perfectly balanced configuration. Another measure of overall balance of a structure is the center of mass. This is the point in the geometry where it would balance if it was a solid object.
Figure 10 shows a detail view of the central triangle of three different Sri Yantras. The left figure shows a configuration where only concurrency is achieved. In this case the bindu (red dot), the center of the outer circle (green dot) and the center of mass (blue dot) are not aligned.
The central figure shows a Sri Yantra that achieves concurrency and concentricity. As a result the bindu (red) and the center of the outer circle (green) overlap nicely. The center of mass still doesn't overlap however.
On the right we see that for a figure drawn with the three criterion that we have suggested (concurrency, concentricity and equilateral central triangle), the three centers overlap and we have a perfectly centered and balanced figure.
The Sri Yantra from Sringeri Temple
 |
 |
| Figure 11 Sri Yantra from Sringeri temple. |
|
The Sringeri temple in India claims to have the oldest Sri Yantra. This temple is one of the four pillars founded by none other than Shankara during the first millennium. Assuming that older Sri Yantras are closer to the original configuration lets see how this Sri Yantra compares to our optimal version. Obviously it is not possible to be certain that it is the oldest Sri Yantra on Earth but it is certainly older than most of the versions available. The shape of the petals and the bhupura are good indicators that it is a old Sri Yantra configuration.
Figure 11 shows an alleged picture of this Sri Yantra and a diagram that was drawn from the picture. Taking into account the distortions caused by the camera and printing we can see that the figure has many of the same characteristics as our optimal figure. The bindu is well centered and more importantly the centermost triangle has an angle very close to 60 degrees.
The Three Flavors of the Sri Yantra
 |
 |
 |
Plane form |
Pyramidal form (Meru) |
Spherical form (Kurma) |
Since the Sri Yantra is based on triangles it is very appropriate that there are currently three main ways to represent this figure. The first and probably the most common is the plane form, which is what we have been looking at so far. More pictures of the plane form can be seen here.
The second is the pyramidal form called Meru in India. Mount Meru is a mythical mountain. So named because of the mountain shape of the figure. More pictures of pyramidal Sri Yantras can be seen here.
The third and rarest form is the spherical form or Kurma. Kurma was the second incarnation of Vishnu, the turtle incarnation. This refers to the similarity between this form and the shell of a turtle. It is interesting to note that there seems to be some confusion with the use of these two terms. The pyramidal form is often wrongly referred to as Kurma. This form is the rarest because of the extremely high level of difficulty involved in generating it. We have not yet found a correct physical representation of a spherical Sri Yantra. There are many attempts but very few have succeeded. Pictures of spherical Sri Yantras can be seen here.
As we have mentioned earlier, drawing a Sri Yantra with minimal errors at the intersections is in itself a good challenge. If on top of that we add the two additional criterion that we have proposed (concentricity, and equilateral inner triangle) then it would probably take a lifetime of trials and errors to achieve such a figure. But thanks to computers and mathematics this can be achieved in the blink of an eye. To achieve this result however, the figure needs to be converted into a simultaneous equation and then solved for the required constraints. For more on this topic take a look at the excellent paper from C.S. Rao. Once this is done we can then shape the figure according to the different criterion described above to obtain an optimal figure where the errors at the intersections are minimal, the figure is perfectly centered and the innermost triangle is equilateral.
|





